The Monty Hall Problem: A Statistical Illusion
- Justine Gaw
- Jan 30, 2023
- 4 min read
Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say Door No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?
This question, published in Parade magazine, has plagued both civilians and mathematicians alike. The answer that the majority of the population will come up with will probably be “It’s a fifty-fifty chance,” and many will choose to stay with their original choice for fear that the game host is simply manipulating them. In reality, switching your choice has the highest probability of getting you a car. Confused? You’re not alone.
Normally we’d think that opening a door removes it from the equation and leaves you with only two doors, but this is a special sort of problem. Although you cannot choose the door that has been opened, it still remains in the equation. Simply put, you started out with a ⅓ chance of getting the answer right, and by opening the door, the game host eliminates the possibility of you opening one door, therefore reducing the fraction to ½, or at least in your perception. However, you neglect to take into account that your mental calculations do not match up with the equation in real life. You are given more information than can be numerically represented in the equation, translating to you making assumptions that could not be created. This is where the statistical illusion comes into play. At its core, this problem is confusing because it plays a psychological trick on you, deceiving you into adding and eliminating variables that do not exist in the corporeal world.
Note that we must make the preliminary assumption that everything that the host does is planned out and that he has more information than us. This is represented in the equation by maintaining the same amount of doors all throughout due to this extra information, not entirely eliminating any of them. Recall that even though the game host has more information than you do, his opening a door does not make it disappear into mathematical thin air. The host himself plays a part in the statistical illusion, opening not a random door but a specific door that he knows has the goat in it. The door is opened based on the door that the participant initially chose.
There are numerous ways to overcome this statistical illusion and simply explain this problem and visualize it, with different ways working the best for different people. The first and most popular trick is to extremify the situation. Instead of three doors, it is one hundred doors that you have to choose one car from, surrounded by ninety-nine goats. Picking a door from there would be a completely random endeavor, so when the game host eliminates the other ninety-eight doors, it seems more feasible to switch, since he knows which one has the car behind it and you don’t. You are then more likely to trust the host and not your guesswork. Although the three doors are much less extreme, the higher probability still stands.
The second most popular way to solve this is the Parade Magazine Solution. The solution is to list out the three different order permutations of this problem. You can have a table similar to this:
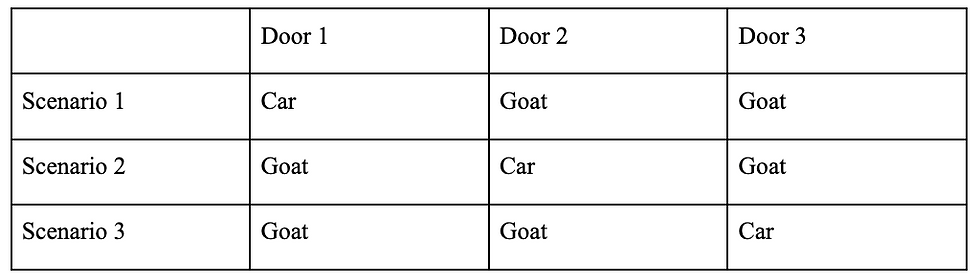
Say that your initial choice is always represented as Door 1 and the game host cannot open a door with a car behind it. The results will then be as follows:
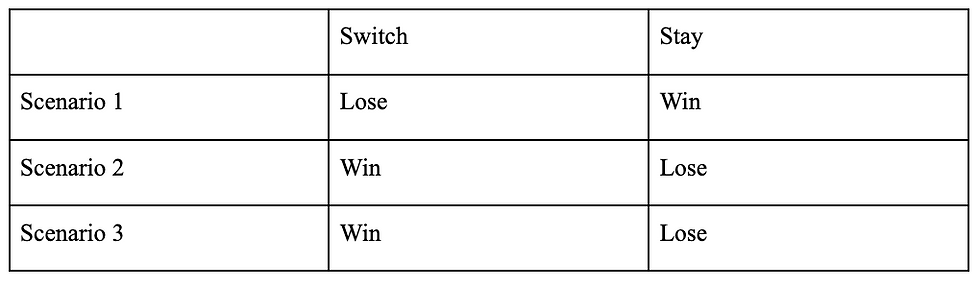
Note that ⅔ of the time, you will win if you switch your choice. The concept behind this is that if you identify that you will win with your first choice for ⅓ of the time while losing with your first choice for ⅔ of the time. On the other hand, you will lose with your second choice ⅓ of the time and win with your second choice for ⅔ of the time. This concept essentially flips the problem on its head and gives a visual and simple explanation of why it works, integrating the extra information that the game host has into the problem by simply stating that he cannot open a door with a car behind it.
A solution that I personally think reconciles the issue between the ½ misconception and the ⅔ statistical reality is that the ½ misconception groups the unpicked door and the door that the game host picked together as one choice. Recall that the main misconception came from the thought that our inability to pick the door that the game host opened removed it from the equation. However, this isn’t the case. Think of the doors and the choices that you make as separate. There are two choices: to switch or to stay. There are three doors: one that you picked, one that is untouched, and one that the game host opened. The untouched and opened doors are grouped together because if you make the choice to switch, you effectively choose both those doors because they both make an impact on the choice. The game host will always reveal a goat and is simply narrowing down your choices, not the doors themselves.
The essence of this statistical illusion is in the information that the game host holds, which cannot be truly represented mathematically outside of this context. Furthermore, note the lack of mathematical equations in the above solutions. There can be cold, hard math in this situation, but in my opinion, it takes away from the intricacies of the illusion and why it is an illusion in itself, bypassing all the elements that make this problem such an iconic puzzle. Looking at the array of solutions presented and the many more that float around the internet, the beautiful thing about this problem is that each person will understand it and explain it differently. Perhaps solutions like extremifying the situation and drawing tables will start you off on the right track, but to truly understand the problem in the way that works best for your brain is something that you will have to search for yourself.




Comments